The method I’m going to tell about is a part of invented in late USSR EMKO system. It was developed specifically to use with computers so it doesn’t have “use a french curve” instructions and things like that. Isn’t that nice?
The main idea is to break down all the curves into arcs with defined center and radius. Here is how I use it in Valentina.

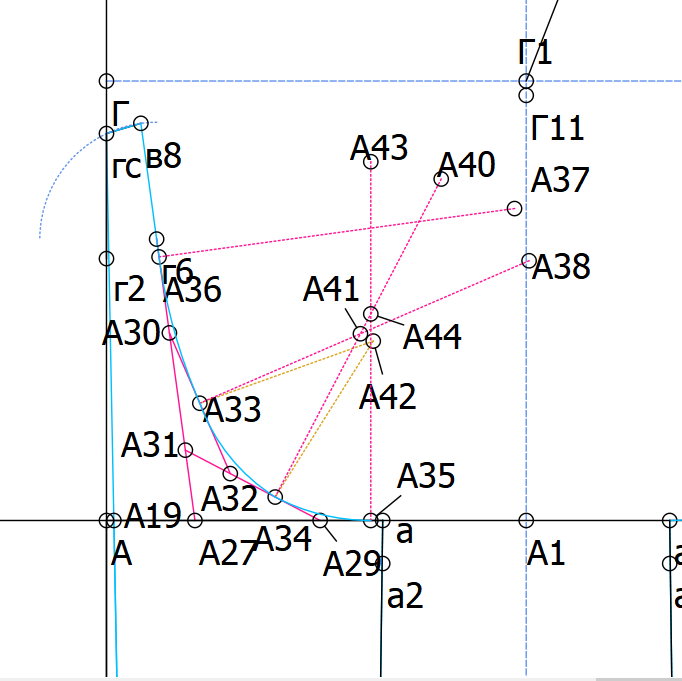
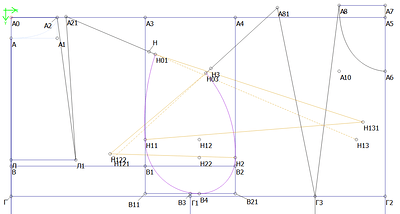
That’s what we start with. Н01 and H03 are shoulder points, B11_B21 is the bottom line of the armhole
- The first thing we do - find points where armhole touches the bottom line and vertical lines
Line_B11_B4 = Line_B11_B21 * 0,6 (on B11_B21)
Line_B11_H11 = Line_B11_B4 (up vertically)
Line_B12_H2 = Line_B4_B21 (up vertically)
That will be start and end points of the first two arcs
- Find center points. These two arcs are always 90° so their center points may be easily found using “point from X and Y of two other points” tool
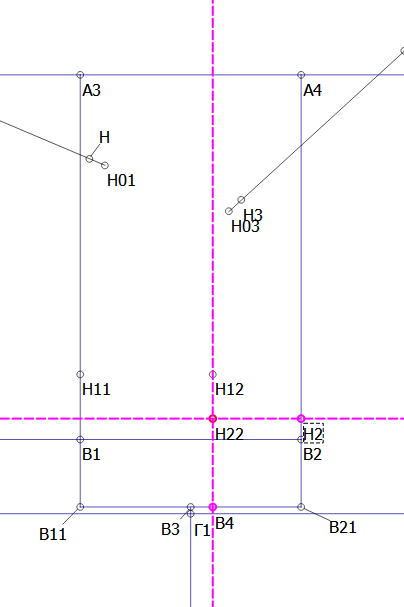
- Now draw the arcs.
Arc tool, center point H12, radius Line_В11_В4, first angle 180, second angle 270
Arc tool, center point H22, radius Line_В4_В21, first angle 270, second angle 360 or 0
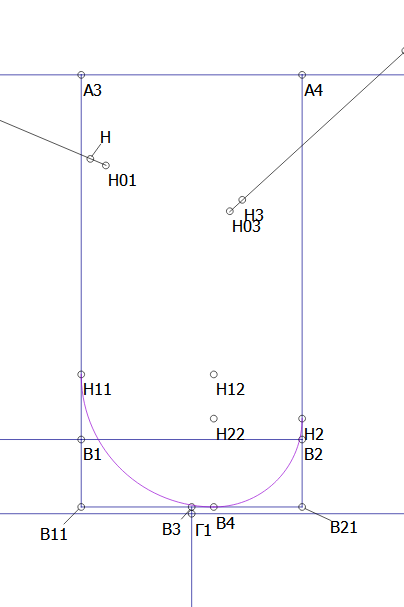
- Now find center points for other two arcs. Find the intersection point of back shoulder line (A21_H01 in my drawing) with H11_H12. Connect the point you got (H13) with H01. Line_H13_H01 is radius of two intersecting circles with centers in points H11 and H01. The point of intersection is the center of the third arc. (Н131)

-
The next thing is finding the angles of the arc. This time 90 * x won’t work) We will use AngleLine option in formulas, so we need to draw lines with needed angles. Just connect Н131 with H11 and H01 (Make sure to click H131 first)
-
Finally, draw the arc
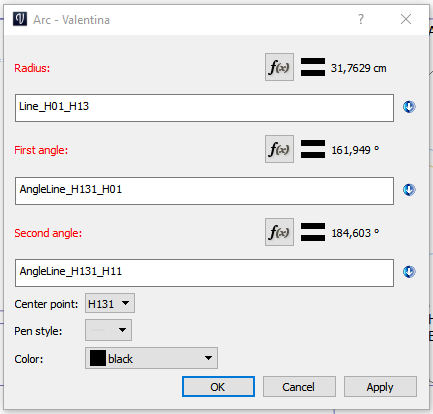
- The process is similar for the last arc. Find a point of intersection of A81_H03 and H2_H22 (point H121). Use H03_H121 as the radius of two circles (centers are H2 and H03). Connect center point with start and end points. Draw an arc.
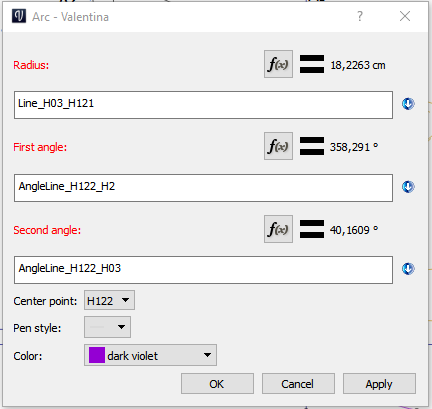
That’s it! A little messy (I wish I could use AngleLine without actually connecting the points) but it scales perfectly with different measurements or when you need to make armhole longer, for example.

 Thank you, I’ll give it a try, too.
Thank you, I’ll give it a try, too.